[알고리즘] Dynamic Programming(동적 계획법)-정의, 피보나치 수열

동적 프로그래밍이란 큰 문제를 작은 부분 문제로 분해하여 해결하는 방법이다. 이렇게 하면 각 부분 문제의 해답을 여러 번 반복하지 않아도 되므로 전체 문제를 훨씬 빠르게 해결할 수 있다.

이 방법은 문제가 두 가지 특성을 가질 때 잘 작동한다:

최적 부분 구조(Optimal structure)
최적 부분 구조는 전체 문제의 최적 해답이 그 부분 문제들의 최적 해답에서 구성될 수 있음을 의미한다.

중복되는 부분 문제(Overlapping Subproblems)
중복되는 부분 문제는 동일한 부분 문제가 여러 번 반복되는 경우를 의미한다.

피보나치 수열을 예로 들어보자.

수열의 n번째 항을 구할 때, 재귀는 아주 쉬운 방법이다.

아래는 재귀를 이용해 파이썬으로 구현한 피보나치 수열이다. 

그런데 이 알고리즘은 시간복잡도가 너무 높다. 시간이 너무 오래 걸린다는 말이다.

예를 들어, fibonacci(5)를 생각해보자.

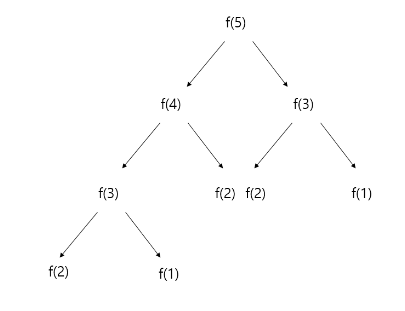
위의 그림과 같은 과정을 거친다. 그림에서 f(1), f(2), f(3)의 연산이 중복되는 것을 알 수 있다.

f(1), f(2), f(3)의 결과를 어딘가에 저장해놓고 사용한다면  이러한 연산을 다시 수행할 필요가 없다! 이것이 바로 메모이제이션(memoization) 이다.

메모이제이션은 동일한 문제를 반복해야 할 경우, 미리 계산해서 저장해 둔 결과를 활용하여 중복 연산을 줄이는 방식을 말한다. 동적 프로그래밍은 메모이제이션을 이용하여 중복되는 부분 문제를 효과적으로 해결할 수 있다.

동적 프로그래밍을 사용하는 두 가지 접근법이 있다:

Top-down 방식과 Bottom-up 방식

1. Top-down 방식
1) 큰 문제를 작은 문제(하위 문제)로 나눈다.
2) 작은 문제(하위 문제)를 푼다.
3) 작은 문제의 답을 결합해 최종 문제를 해결한다.

피보나치 수열을 예로 들어 보자:

1) 큰 문제를 작은 문제(하위 문제)로 나눈다.
-문제를 fibonacci(n-1)과 fibonacci(n-2)로 나눈다.

 

2) 작은 문제(하위 문제)를 푼다.
-fibonacci(n-1)과 fibonacci(n-2)를 계산한다. 이 값들이 이미 계산되었다면 저장된 값을 사용한다. 그렇지 않으면 이 값을 메모이제이션 배열(dp 배열)에 저장한다.

 

3) 작은 문제의 답을 결합해 최종 문제를 해결한다.
-fibonacci(n-1)과 fibonacci(n-2)를 더해 fibonacci(n)을 계산한다.

이를 Python 언어로 구현하면 다음과 같다.

2. Bottom-up 방식
Bottom-up 방식은 먼저 작은 문제들을 해결하고 그것들을 결합하여 큰 문제를 해결하는 방식이다.
1) 작은 문제들부터 해결한다.
2) 작은 문제들의 답을 이용해 큰 문제를 해결한다.
3) 이 과정을 반복해 최종 문제를 해결한다.

피보나치 수열을 예로 들면 다음과 같은 과정을 거치게 된다:

1) 작은 문제들부터 해결합니다.
-fibo(i-1), fibo(i-2)에 대응하는 dp[i-1], dp[i-2]를 계산한다.

 

2) 작은 문제들의 답을 이용해 큰 문제를 해결한다.
-dp[i-1] + dp[i-2]를 이용해 dp[i]를 계산한다.

 

3) 이 과정을 반복해 최종 문제를 해결한다.
-이 과정을 반복하여 dp[n]을 계산한다.

 

이를 Python 언어로 구현하면 다음과 같다.

피보나치의 경우에는 Bottom-up 방식으로 해결하면 재귀 함수 호출로 인한 오버헤드가 없어서 Top-down 방식에 비해 더 효율적이다.